How to Read a T Table Stats
Given below is the T Tabular array (also known as T-Distribution Tables or Educatee's T-Table). The T Table given below contains both one-tailed T-distribution and two-tailed T-distribution, df upward to m and a confidence level up to 99.9%
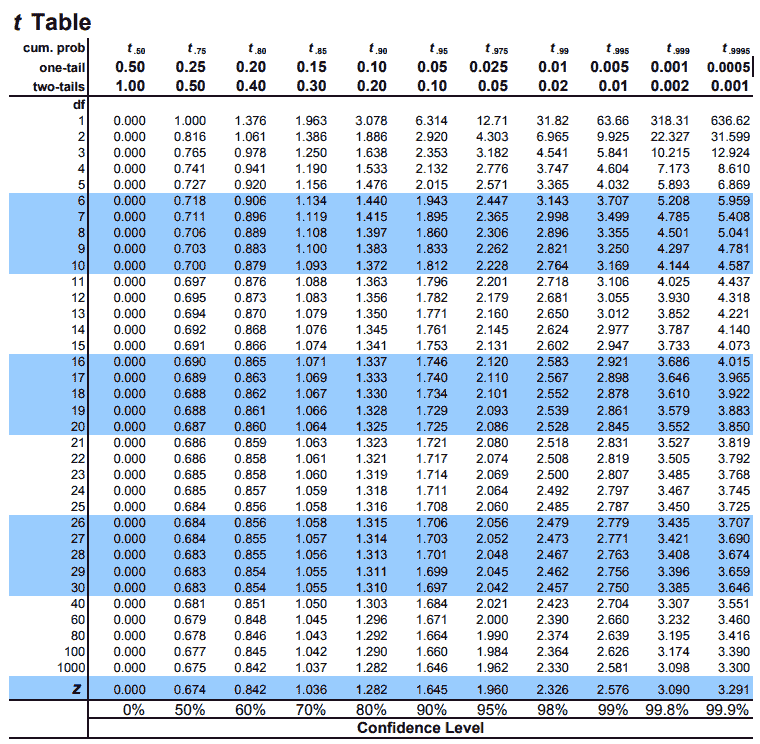
Free Usage Disclaimer: Experience free to use and share the above images of T-Tabular array every bit long as you provide attribution to our site by crediting a link to https://www.tdistributiontable.com
How to Use the T-Table
Next, we are going to learn how to read the T-Table and map critical values on it using examples and diagrams but first we volition demand a few things or pre-requisites before we tin can practise that.
The pre-requisites required to using a T-table are:
- The number of tails: Nosotros demand to know whether our t-test is one-tailed or two-tailed because we will use the respective 1-tail or two-tail row to mark the alpha level. The alpha levels are listed at top of the tabular array (0.50, 0.25, 0.20, 0.15…for the one-tail and 1.00, 0.50, 0.40, 0.30…for the two-tails) and as y'all can see they vary based on whether the t-test is one-tail or 2-tails.
- Degrees of freedom: The degrees of freedom (df) bespeak the number of independent values that tin can vary in an analysis without breaking any constraints. The degrees of freedom will either be explicitly mentioned in the problem statement or if it is not explicitly mentioned, all yous have to practice is subtract ane from your sample size (north – 1) and what you go will be your df or degrees of liberty.
- Alpha level: The alpha level ( α ), also known as the significance level is the probability of rejecting the null hypothesis when it is truthful. The common blastoff levels for t-examination are 0.01, 0.05 and 0.10
One time you lot have all three, all yous have to do is option the respective column for one-tail or ii-tail from the table and map the intersection of the values for the degrees of freedom (df) and the alpha level.
Let us sympathise how to read the T-Table using an example of an one-tailed test.
Case: Let'southward say we want to map an ane-tailed t-test for a mean with an alpha level of 0.05. The total students involved in this report are 25. What critical value should we compare t to?
Answer:
- Firstly, we see that at that place are 25 students involved in this written report. To go the degrees of freedom (df), we take to subtract 1 from the sample size. Therefore, df = n – one = 25 – 1 = 24.
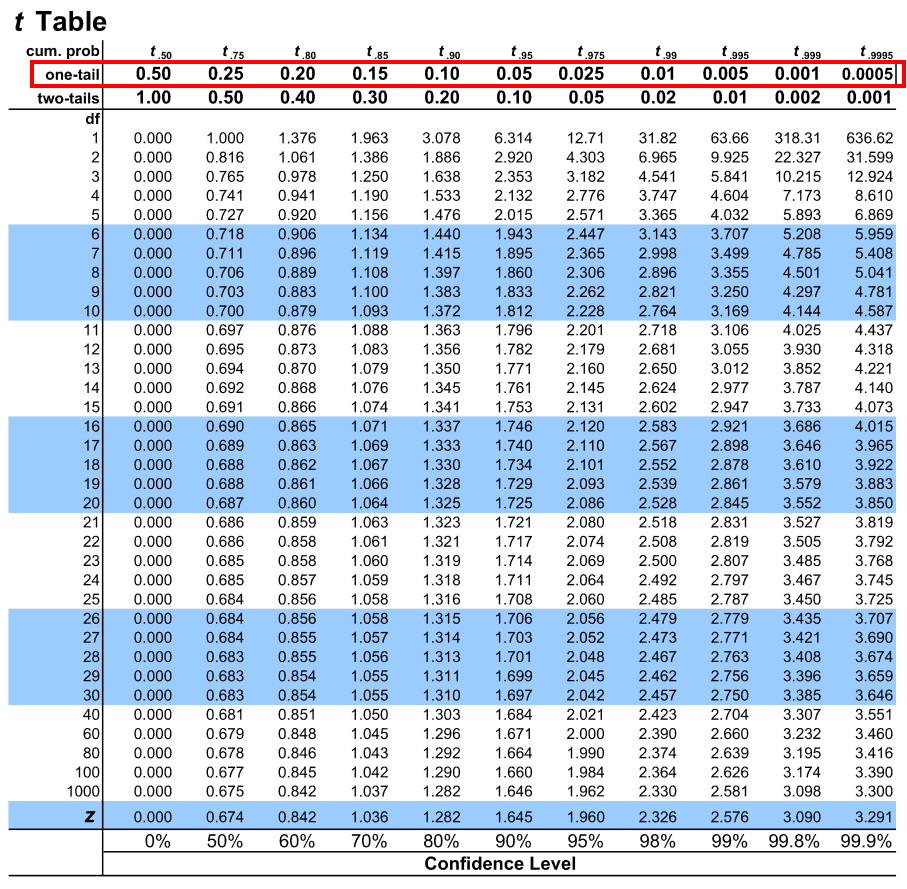
2. Side by side, nosotros run into that our t-test is one-tailed. So we will cull the one-tail row to map our alpha level.
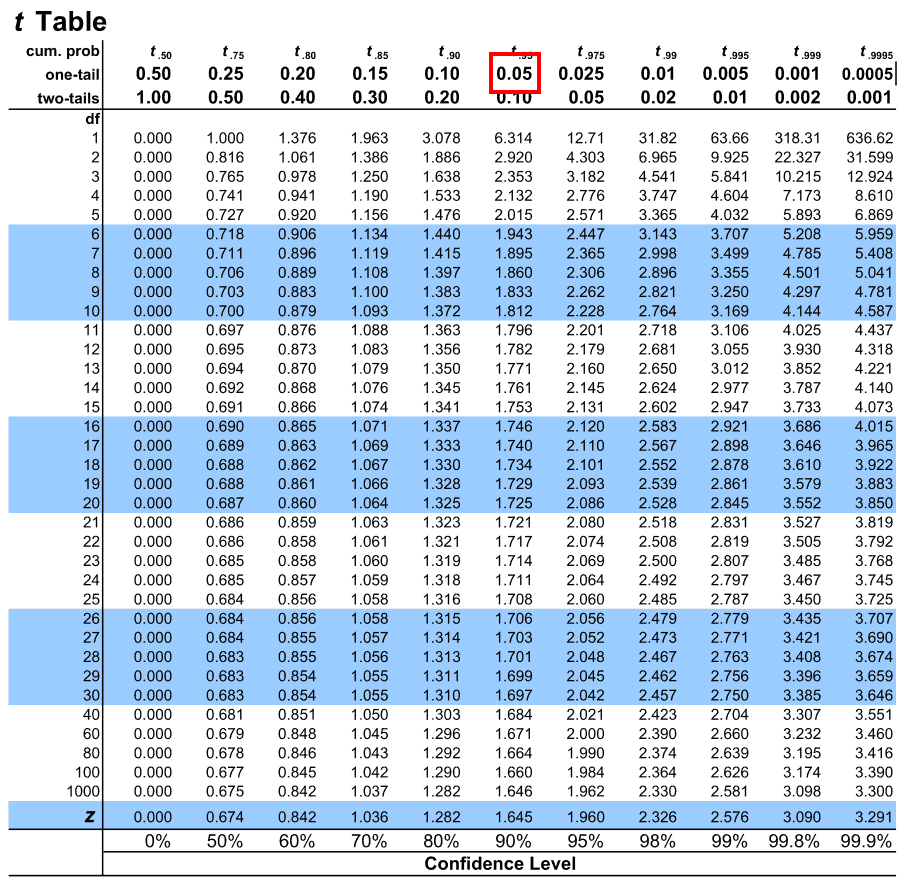
3. Next, nosotros look for the alpha value forth the above highlighted row. Our alpha level for this example is 0.05. Allow us map the same on the table
4. Once that is done, let us map the degrees of freedom under the leftmost column of the table under (df)
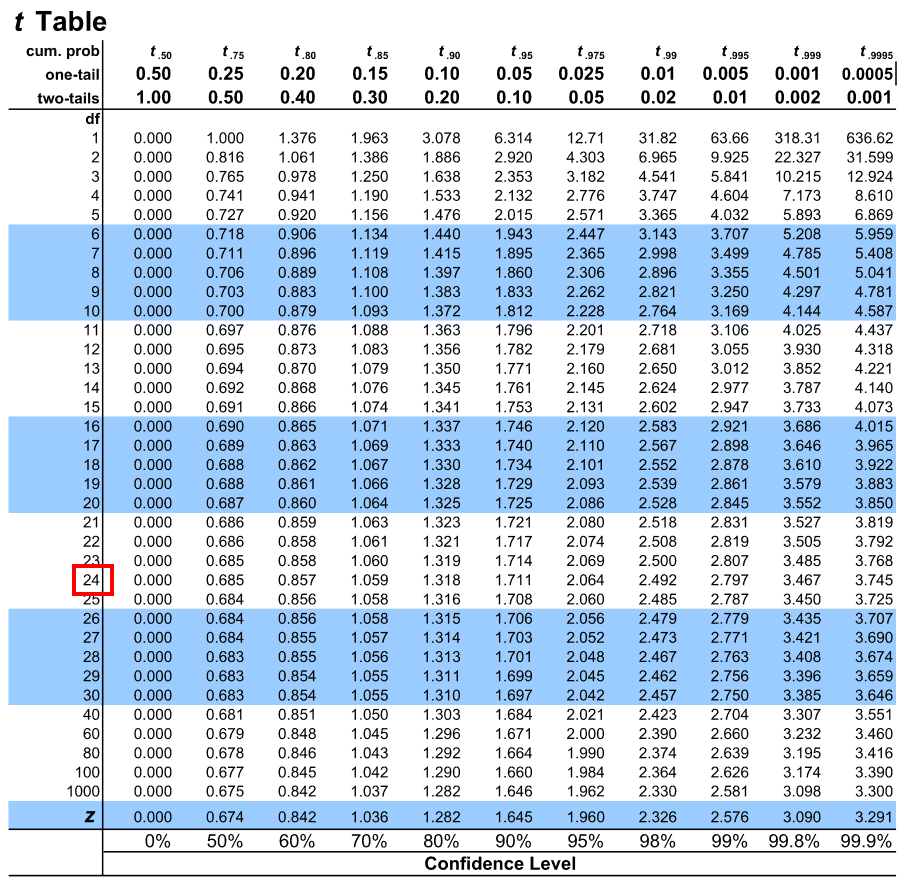
5. The intersection of these two presents us with the critical value we are looking for
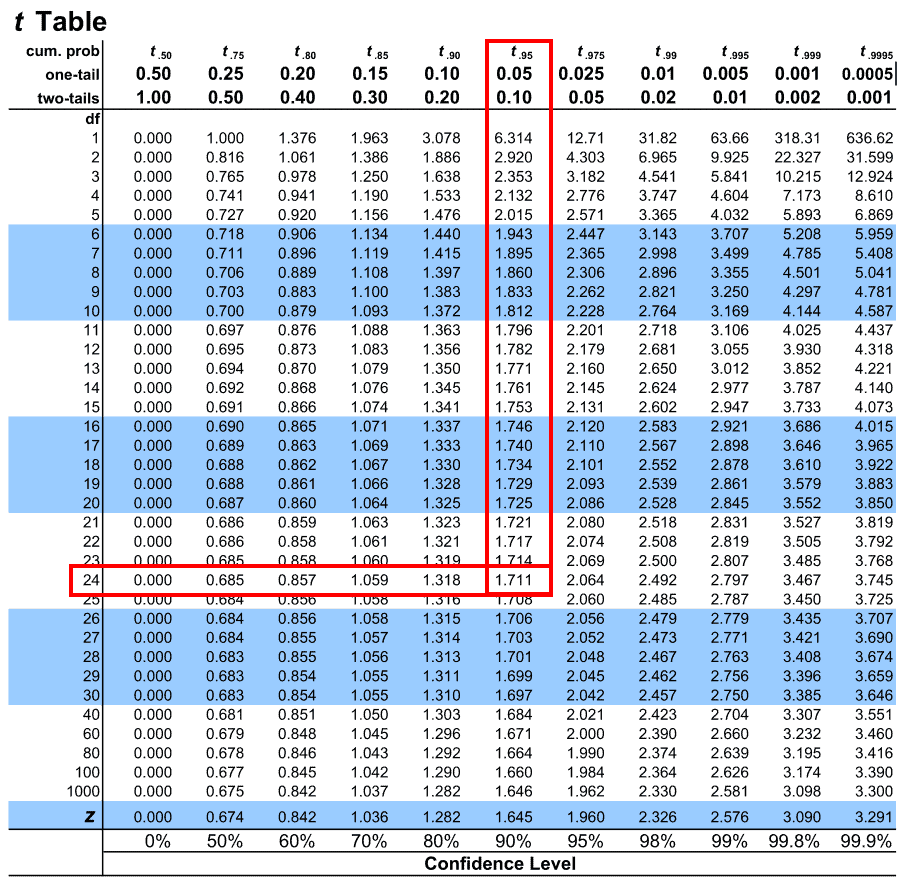
Hence we see that the critical value corresponding to our t in the t-distribution table is 1.711.
In a similar way, you can also map critical values for 2-tailed tests with the only departure existence that you have to select the two-tailed row of alpha values instead. The balance of the steps are the aforementioned.
Sample Questions
Following are some sample questions for your practice.
Question i: For a 2-tailed test with an alpha level of 0.30 and 18 every bit the sample size, what is the critical value we should compare t to?
Solution: Nosotros can deduce the following from our problem statement. The sample size is xviii. Therefore the degrees of freedom ( df ) = 18 – 1 = 17. We tin as well encounter that the exam is two-tailed and has an alpha level of 0.30. And so on the T-Table, nosotros map the column for two-tailed alpha values first and and then map the value 0.xxx across information technology. Then we map the value 17 under the left-most column 'df' and the intersection of these 2 is our answer which is 1.069
Question two: For an 1-tailed test, the sample size if 23. What is the degrees of freedom?
Solution: Degrees of liberty ( df ) = due north – 1 = 23 – 1 = 22
Question 3: A research study conducts an one-tailed examination with an alpha level of 0.ten and a sample size of 12. What critical value should exist compared to the t value obtained every bit the test statistic?
Solution: The sample size is 12. Hence the degrees of freedom ( df ) = 12 – 1 = 11. Mapping the alpha level beyond the row for one-tailed alpha values and the df of 17 on the left-side of the table, nosotros get our disquisitional value as 1.363
When is T Distribution used?
T Distribution is used when you accept a small sample size because otherwise the T Distribution is almost identical to normal distribution with the only divergence existence that the T distribution curve is shorter and fatter than normal distribution curve
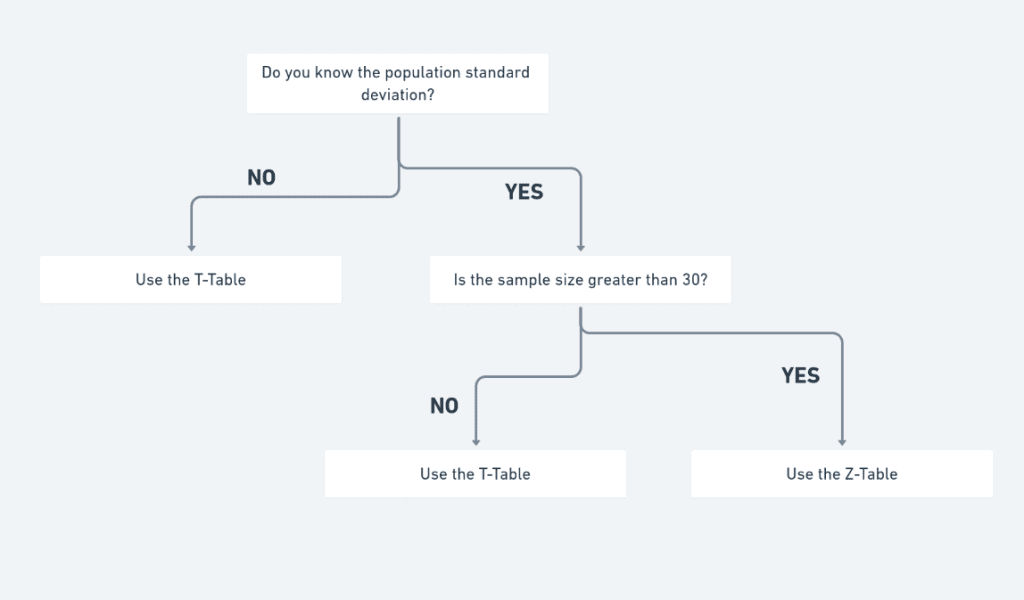
T Table vs Z Table vs Chi Square Table
The T distribution, Z distribution and Chi Squared distribution are few of the most ordinarily used probability distribution patterns and information technology is important to know the differences betwixt them and when to employ which distribution pattern
Unremarkably a Z Table is used when the population standard deviation and mean are known. Whereas a T Table is used when the T score is calculated without the knowledge of the mean and the population standard deviation. Generally T Table is too preferred over the Z Table to be used when the sample size is small (N<30)
A chi foursquare distribution on the other hand, with k degrees of freedom is the distribution of a sum of squares of 1000 contained standard normal variables. And is used in test for the independence of 2 variables in a contingency tabular array and for tests fir goodness of fit of an observed data to see if information technology matches to a theoretical one.
What is one tail vs 2 tail?
Let us empathise offset what a 'tail' is when it comes to t distribution and then let the states figure out when to employ a one-tailed t exam vs two-tailed t examination.
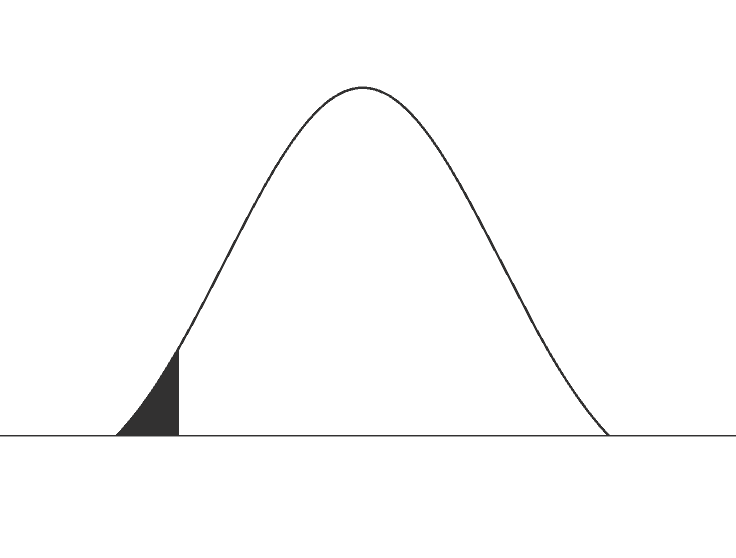
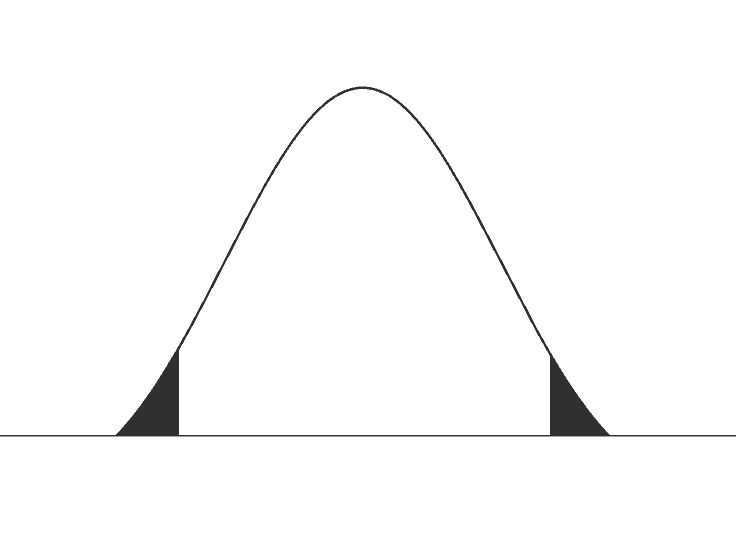
The 'tail' in terms of whatsoever distribution refers to end of the distribution of the test statistic. As you can run across in the image aslope, the black shaded areas of the distributions are the tails. In the image where both the ends of the distribution is shaded it is said to be 2-tailed and where only i end of the distribution is shaded, information technology is one-tailed. Unremarkably distribution patterns similar t distributions and z distributions are two tailed. Whereas asymmetrical distributions similar Chi-foursquare distributions and F distribution will have only one tail. One-tailed tests are besides known equally directional tests whereas two-tailed tests are also known equally non-directional tests.
So how do yous choose whether you want to use a one-tailed t test or a two-tailed t test? A simple way to determine that is by checking if you want to use both the negative and the positive end of the distribution (apply two-tail) or if you just desire to use a 1 directional comparison (use i-tail)
For example if you want to desire to check whether Group A is both taller and shorter than Group B, and so you must utilize a two-tailed exam. Whereas if you merely want to see if Grouping A is taller than Group B but without whatever interest in checking if Group A is shorter than Group B, then utilise a ane-tailed exam.
Merely if you are in dubiety and are unsure if whether you should use a one-tailed examination or a two-tailed exam, then it is better to get with a 2-tailed exam generally.
T statistic formula or T Score formula
T statistic = (Sample mean – hypothesised hateful)/sample standard error
Hence we can see that how large or how small the T statistic is depends on how close or far away the sample mean is from the hypothesised mean. If the sample mean is close to hypothesised mean, we will get a T statistic close to zero. Whereas if the sample hateful if far away from the hypothesised mean, we will go a larger T statistic.
Why is T Tabular array called as Student's T Table or Student's T Distribution?
The term 'Student' has naught to practice with the literal term student every bit used in the English language language per se. But rather from William Sealy Gosset to whom the T-distrubtion is attributed to. William Sealy Gosset's pen name 'Student' was used in 1908 to publish the distrubtion for the first time in 1908 in the paper Biometrika. The Student'due south t-distribution was also initially referred to as 'Student's Z' and 'Pupil's test of statistical significance' before being usually called Student'south t-distribution as information technology is known today.
History of T Table

Both the t-statistic and the t-distribution were discovered around the nineteenth century. T-distribution was first penned by Helmert and Lüroth in the year 1876. Friedrich Helmert born in the year 1843 in Kingdom of Saxony penned 'Die mathematischen und physikalischen Theorieen der höheren Geodäsie' which formed the foundation of modern Geodesy.

Jacob Lüroth born in 1844 in Germany was a mathematician known for proving Lüroth'due south theorem, for introducing Lüroth quartics and his thesis on Pascal's theorem. Although the discovery of T-distribution is credited to William Sealy Gosset, it is believed Helmert and Lüroth played a primal part and derived it first. The t-distribution is also plant in Karl Pearson'southward 1895 newspaper but in a very general form known then as the Pearson Type Four.

The t-statistic however is named afterwards and attributed to William Sealy Gosset. Gosset was born in 1876 was the Head Brewer at Guinness and is considered the father of modern British statistics. The t-statistic was introduced by William Gosset in the yr 1908 under his pen name 'Student'.
The distribution was first published in 1908 paper in Biometrika under his pseudonym 'Educatee'. Hence, Student's t-distribution gets it'southward proper name from his pseudonym 'Student' and has zip to do with the literal term student equally used in the English language language. The Student's t-distribution was also initially referred to as 'Student's Z' and 'Student's examination of statistical significance' earlier being usually called Educatee's t-distribution as information technology is known today.
Tags: T table, t distribution table, t distribution, t nautical chart, t-table, t score calculator, t score tabular array, t statistic, t score, t exam tabular array, t value, t value table, t table statistics, t tabular array calculator, t-distribution table,t-distribution,t-statistic,t-chart, ttables, t tables, t chart stats, t nautical chart statistics, t critical value, t score chart, t disquisitional value table, pupil t tabular array, total t distribution tabular array, t-value, t exam chart,student's t table, ttable, t test, students t exam,
Source: https://www.tdistributiontable.com/
0 Response to "How to Read a T Table Stats"
Postar um comentário